Chào mừng các bạn đã quay trở lại với hệ thống bài học của chúng tôi. Hôm nay, chúng ta sẽ cùng nhau khám phá một chủ đề hình học thú vị và quan trọng: cách nhận biết và vẽ các đường thẳng song song, vuông góc. Đây là kiến thức nền tảng giúp các em học sinh xây dựng tư duy không gian và giải quyết nhiều bài toán phức tạp hơn sau này.

Tổng Quan Về Đường Thẳng Song Song Và Vuông Góc
Trong hình học, hai đường thẳng có thể có các vị trí tương đối khác nhau. Hai trong số những vị trí phổ biến và dễ nhận biết nhất chính là song song và vuông góc. Hiểu rõ đặc điểm của chúng là bước đầu tiên để chinh phục thế giới hình học.
- Đường thẳng song song: Là hai đường thẳng nằm trong cùng một mặt phẳng và không bao giờ cắt nhau, dù có kéo dài đến đâu. Chúng luôn cách đều nhau. Ví dụ, hai thanh ray xe lửa chính là hình ảnh trực quan của hai đường thẳng song song.
- Đường thẳng vuông góc: Là hai đường thẳng cắt nhau tại một điểm và tạo thành 4 góc vuông (góc 90 độ). Góc vuông là góc có hình dạng giống như góc của một tờ giấy, một chiếc bàn hay khung cửa sổ.
Việc nắm vững lý thuyết này sẽ giúp các em dễ dàng hơn khi bước vào phần thực hành vẽ hình.
Hướng Dẫn Vẽ Hai Đường Thẳng Song Song
Chúng ta sẽ bắt đầu với bài tập vẽ hai đường thẳng song song, chẳng hạn như đường thẳng AB song song với đường thẳng CD.
- Bước 1: Vẽ đường thẳng thứ nhất. Trước tiên, hãy vẽ một đường thẳng và đặt tên là AB. Đây sẽ là đường thẳng mẫu.
- Bước 2: Xác định khoảng cách. Sử dụng thước kẻ để xác định một khoảng cách cố định từ đường thẳng AB. Khoảng cách này chính là “đường cao” hay khoảng cách giữa hai đường thẳng song song.
- Bước 3: Vẽ đường thẳng thứ hai. Dựa vào khoảng cách đã xác định, vẽ một đường thẳng khác sao cho mọi điểm trên đường thẳng này đều cách đường thẳng AB một khoảng bằng nhau. Đặt tên đường thẳng này là CD.
- Kiểm tra: Dùng thước ê-ke hoặc tính chất của hình học để kiểm tra xem AB và CD có thực sự song song không (chúng không cắt nhau và khoảng cách là không đổi).
Khi đã thành thạo, bạn có thể áp dụng nguyên tắc tương tự để vẽ các cặp song song khác, như AD song song với BC. Việc luyện tập thường xuyên sẽ giúp kỹ năng vẽ hình của bạn trở nên chính xác và nhanh chóng hơn. Đây là một kỹ năng quan trọng, tương tự như việc thành thạo các phép tính cơ bản là nền tảng cho toán học.
Hướng Dẫn Vẽ Hai Đường Thẳng Vuông Góc
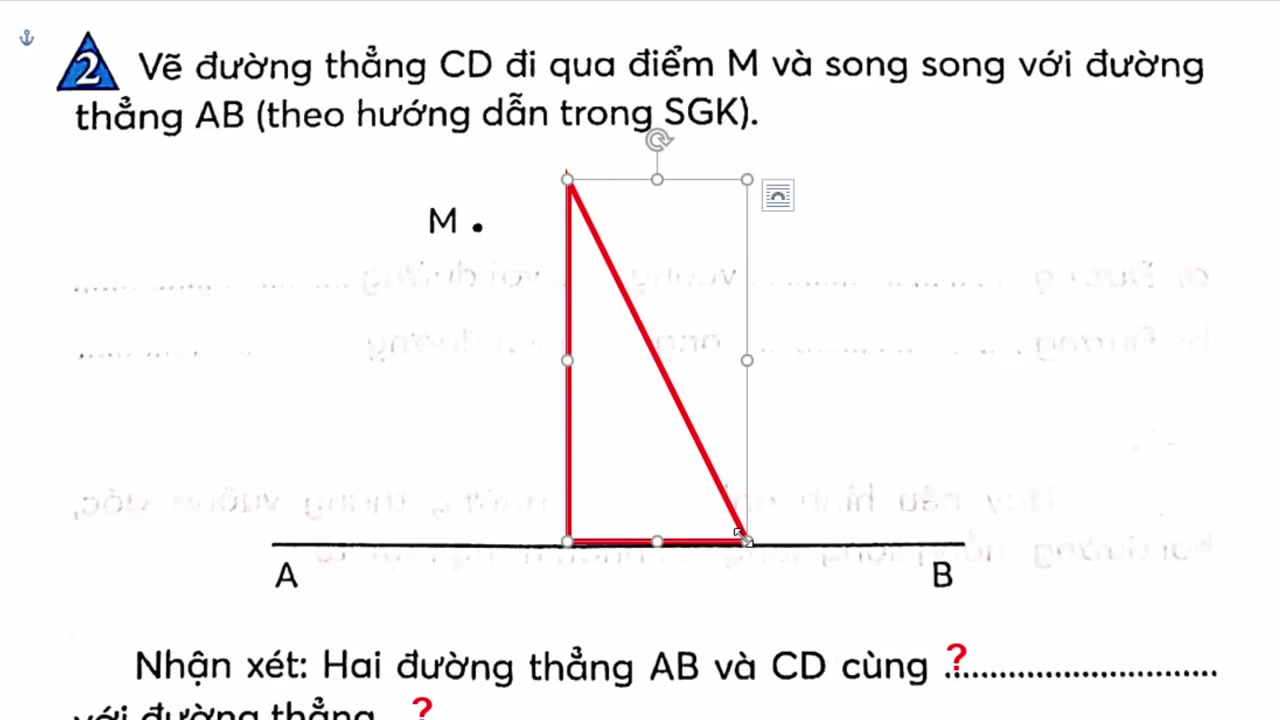
Sau khi đã vẽ được đường thẳng song song, chúng ta chuyển sang một quan hệ khác: đường thẳng vuông góc. Giả sử cần vẽ một đường thẳng đi qua điểm M và vuông góc với đường thẳng AB.
- Bước 1: Đặt thước ê-ke. Đặt cạnh góc vuông của thước ê-ke trùng với đường thẳng AB.
- Bước 2: Trượt thước đến điểm cần vẽ. Giữ nguyên vị trí của thước so với đường thẳng AB, từ từ trượt thước dọc theo AB cho đến khi cạnh góc vuông còn lại của thước đi qua điểm M.
- Bước 3: Vẽ đường vuông góc. Dùng bút chì kẻ một đường thẳng dọc theo cạnh thước đi qua điểm M. Đường thẳng vừa vẽ chính là đường thẳng vuông góc với AB tại M.
- Bước 4: Kiểm tra góc vuông. Bạn có thể kiểm tra lại bằng chính thước ê-ke hoặc bằng cách đo góc tạo thành, đảm bảo nó là 90 độ.
Quá trình này có thể lặp lại để vẽ nhiều đường vuông góc khác nhau, chẳng hạn như vẽ đường thẳng vuông góc với CD. Việc hiểu rõ các mối quan hệ vuông góc và song song là chìa khóa để nhận biết và so sánh các hình dạng trong không gian.
Ứng Dụng Và Bài Tập Nhận Biết Quan Hệ Giữa Các Đường
Lý thuyết sẽ trở nên sống động hơn khi chúng ta áp dụng vào việc quan sát và giải quyết các bài tập thực tế.
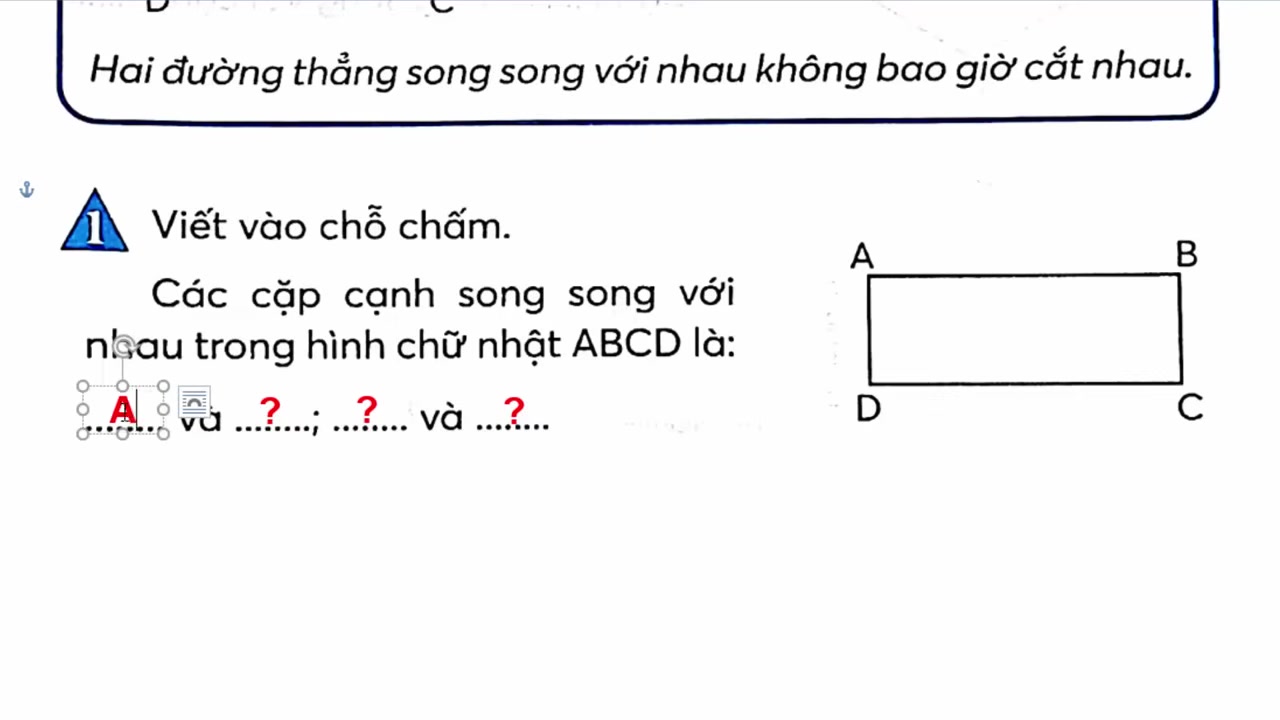
- Quan sát hình vẽ: Khi được cho một hình vẽ có nhiều đường thẳng, hãy tập thói quen quan sát để tìm ra các cặp đường thẳng song song hoặc vuông góc. Ví dụ, trong một hình chữ nhật, bạn sẽ tìm thấy hai cặp cạnh đối diện song song và bốn góc đều là góc vuông.
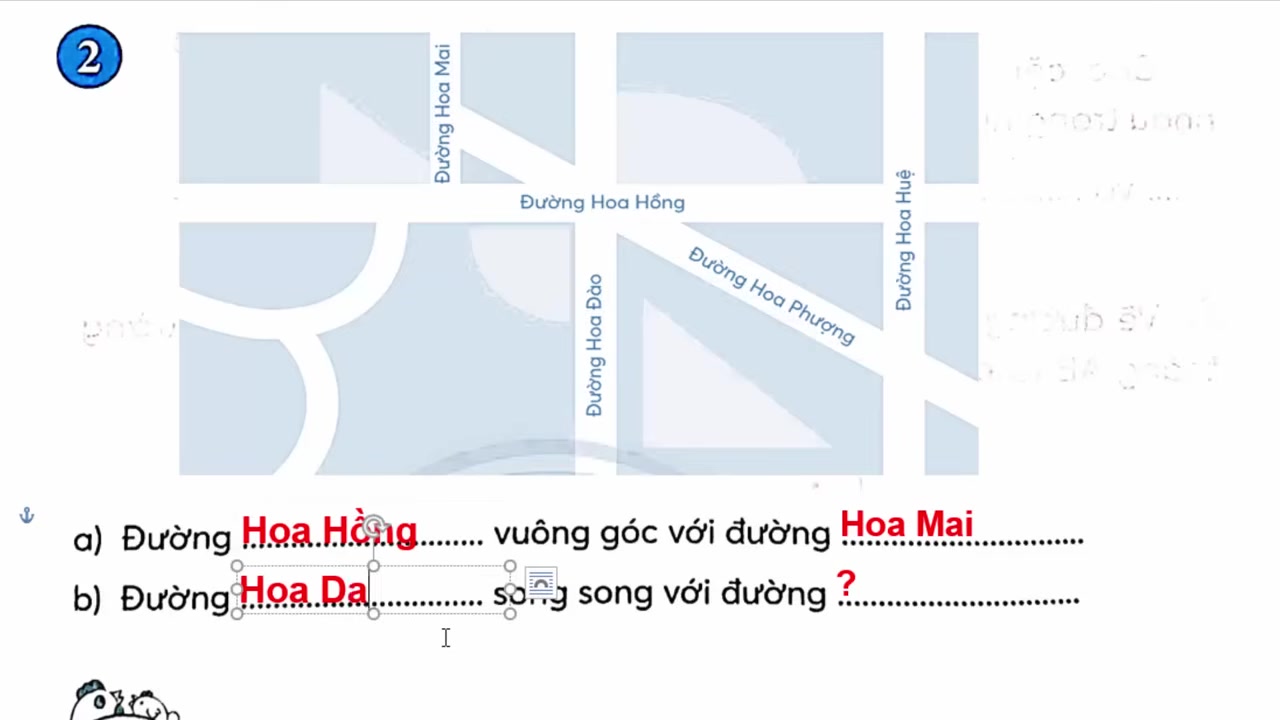
- Bài tập xác định: Một dạng bài phổ biến là cho trước các đoạn thẳng như AB, CD, UV… và yêu cầu chỉ ra đoạn thẳng nào song song hoặc vuông góc với đoạn thẳng nào. Chẳng hạn, AB có thể song song với CD, hoặc UV có thể vuông góc với ST.
- Phân tích từng phần: Đôi khi, bạn cần tách hình lớn thành các phần nhỏ để dễ quan sát. Hãy tìm kiếm các “cặp đôi” có vị trí đặc biệt: hai đường thẳng cùng đi qua một điểm và tạo thành góc vuông, hoặc hai đường thẳng nằm cách đều nhau và không giao nhau.
Việc luyện tập nhận biết này không chỉ giúp bạn làm tốt bài tập trên giấy mà còn phát triển khả năng quan sát thế giới xung quanh. Bạn sẽ thấy hình học hiện diện ở khắp mọi nơi, từ khung cửa, mặt bàn đến những công trình kiến trúc.
Kết Luận
Như vậy, thông qua bài học hôm nay, chúng ta đã cùng nhau ôn tập và thực hành hai khái niệm hình học cơ bản: đường thẳng song song và đường thẳng vuông góc. Từ việc hiểu định nghĩa, các bước vẽ hình chi tiết cho đến kỹ năng quan sát và nhận biết trong các bài tập đều đã được đề cập. Hãy nhớ rằng, thành thạo những kiến thức nền tảng này chính là bước đệm vững chắc để bạn học các phép toán phức tạp hơn như phép chia có dư, vốn cần tư duy logic và phân tích hình học tốt.
Hy vọng video và bài viết này đã mang lại cho bạn những kiến thức bổ ích. Đừng quên luyện tập thường xuyên để kỹ năng của bạn ngày càng thành thạo nhé. Chúc các bạn học tập thật tốt!
