Chào mừng các em đến với bài học toán lớp 2 hôm nay! Trong bài giảng này, chúng ta sẽ cùng nhau khám phá những tính chất thú vị của phép cộng: tính chất giao hoán và tính chất kết hợp. Thông qua các ví dụ minh họa sinh động và bài tập thực hành, các em sẽ hiểu rõ hơn về cách áp dụng chúng để tính toán nhanh và chính xác. Hãy cùng bắt đầu hành trình khám phá này nhé!

Khởi Động Với Tính Chất Giao Hoán
Tính chất giao hoán là một trong những tính chất cơ bản nhất của phép cộng. Hiểu một cách đơn giản, khi đổi chỗ các số hạng trong một tổng, kết quả của chúng ta không hề thay đổi.
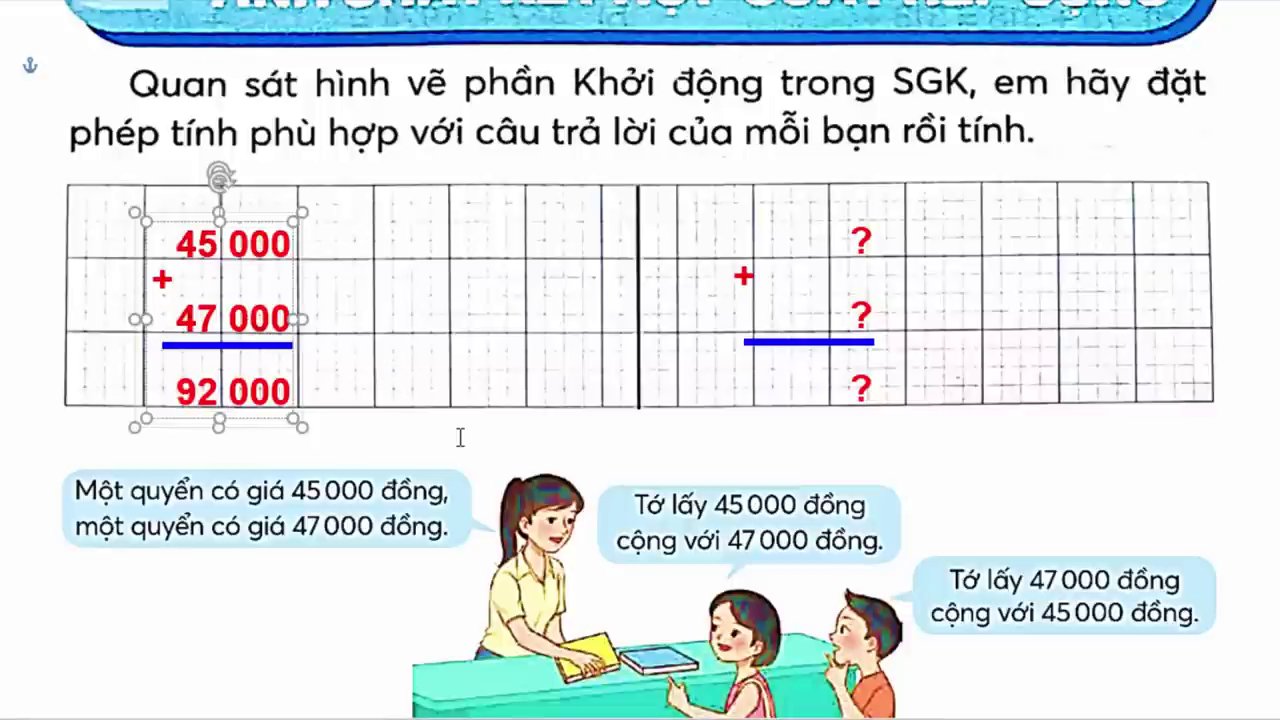
Ví dụ, chúng ta có một quyển sách giá 45,000 đồng và một quyển sách khác giá 47,000 đồng. Tổng số tiền để mua cả hai quyển sách sẽ là:
– 45,000 + 47,000 = 92,000 đồng.
Bây giờ, nếu chúng ta đổi chỗ hai số hạng này và tính:
– 47,000 + 45,000 = 92,000 đồng.
Kết quả vẫn là 92,000 đồng. Điều này chứng minh rằng a + b = b + a. Dù bạn cộng theo thứ tự nào, tổng vẫn giữ nguyên. Đây chính là nội dung cốt lõi của tính chất giao hoán.
Tính chất này không chỉ áp dụng cho số tiền mà còn đúng với mọi con số. Chẳng hạn:
– 45 + 47 = 47 + 45 = 92
– 80,154 + 9,695 = 9,695 + 80,154 = 89,849
Việc nắm vững tính chất này giúp các em linh hoạt hơn khi tính toán, đặc biệt là khi gặp những phép tính phức tạp hơn. Nó là nền tảng quan trọng để các em học tốt các dạng toán sau này, như khi làm quen với phép cộng trong phạm vi lớn hơn.
Tìm Hiểu Về Tính Chất Kết Hợp
Sau khi đã thuần thục với tính chất giao hoán, chúng ta cùng chuyển sang một tính chất quan trọng khác: tính chất kết hợp. Tính chất này cho phép chúng ta nhóm các số hạng lại với nhau theo cách thuận tiện nhất để tính tổng, mà kết quả cuối cùng vẫn không đổi.
Công thức của tính chất kết hợp là: (a + b) + c = a + (b + c).
Điều này có nghĩa là, khi cộng ba số lại với nhau, chúng ta có thể chọn cộng hai số đầu tiên trước, rồi cộng với số thứ ba, hoặc cộng hai số cuối trước, rồi cộng với số đầu tiên. Kết quả cuối cùng vẫn như nhau.
Ví dụ cụ thể:
– (59 + 28) + 12 = 59 + (28 + 12)
– Chúng ta có thể tính: 59 + 28 = 87, rồi 87 + 12 = 99.
– Hoặc có thể tính: 28 + 12 = 40, rồi 59 + 40 = 99.
Cả hai cách đều cho ra đáp án là 99. Tính chất này đặc biệt hữu ích khi chúng ta gặp những số hạng có thể cộng với nhau để tạo thành số tròn chục, tròn trăm. Nó giúp đơn giản hóa các bước tính toán, giảm thiểu sai sót và tính nhanh hơn rất nhiều.

Áp Dụng Tính Chất Vào Giải Bài Tập
Lý thuyết sẽ trở nên dễ hiểu và nhớ lâu hơn khi chúng ta cùng nhau áp dụng vào giải các bài tập thực tế. Dưới đây là một số dạng bài điển hình giúp các em luyện tập.
Dạng 1: Tính Bằng Cách Thuận Tiện Nhất
Đây là dạng bài yêu cầu các em vận dụng linh hoạt cả hai tính chất giao hoán và kết hợp để tìm ra cách tính nhanh và hợp lý.
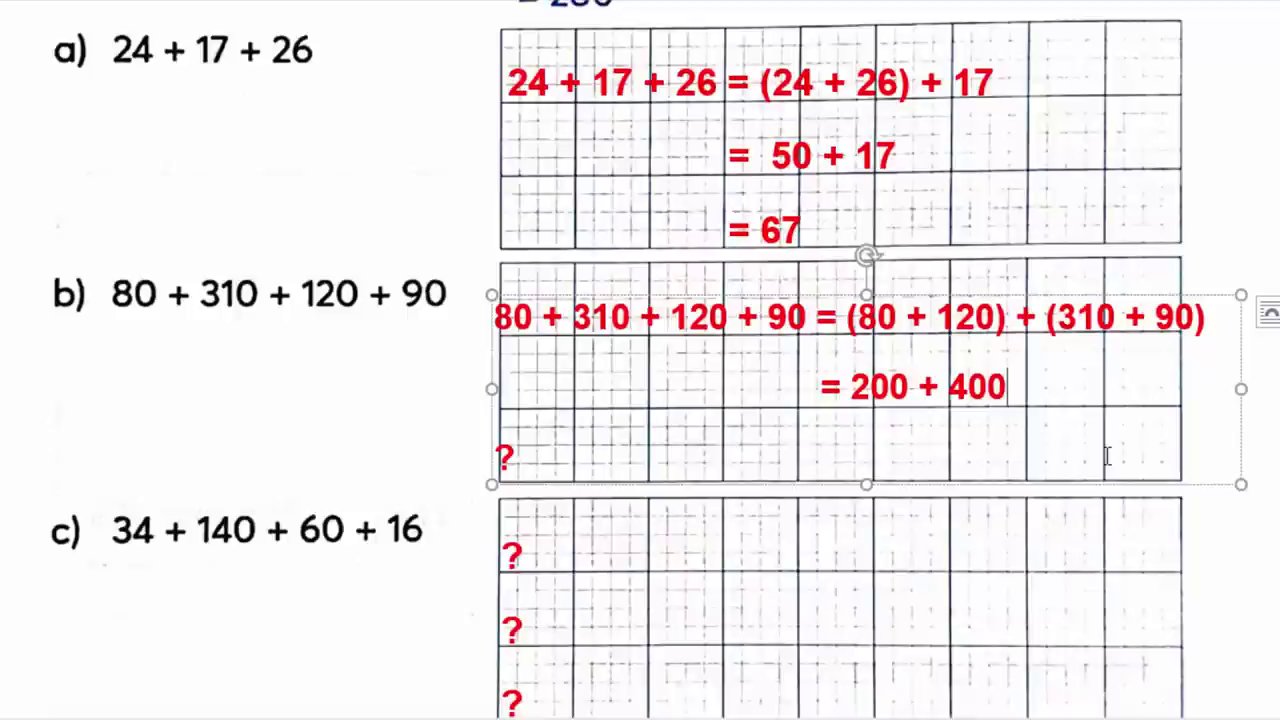
Ví dụ 1: Tính giá trị biểu thức 17 + 148 + 3 + 283.
– Phân tích: Chúng ta thấy 17 và 3 là hai số có thể cộng thành số tròn chục (20). 148 và 283 có thể cộng thành số tròn trăm (431, nhưng chưa thực sự tròn). Tuy nhiên, nếu áp dụng tính chất giao hoán để đổi chỗ, ta có thể nhóm: (17 + 3) + (148 + 283).
– Thực hiện:
1. 17 + 3 = 20
2. 148 + 283 = 431
3. 20 + 431 = 451
– Kết luận: Cách làm này nhanh hơn nhiều so với việc cộng lần lượt từ trái sang phải.
Ví dụ 2: Tính 80 + 350 + 120 + 90.
– Phân tích: Ta thấy 80 và 120 cộng lại được 200 (tròn trăm). 350 và 90 cộng lại được 440.
– Thực hiện:
1. (80 + 120) + (350 + 90)
2. = 200 + 440
3. = 640
Việc nhận diện các cặp số “bạn đồng hành” (cộng vào thành số tròn chục, tròn trăm) là kỹ năng quan trọng. Các em có thể rèn luyện thêm kỹ năng này thông qua các bài tập so sánh và nhận biết số tròn chục.
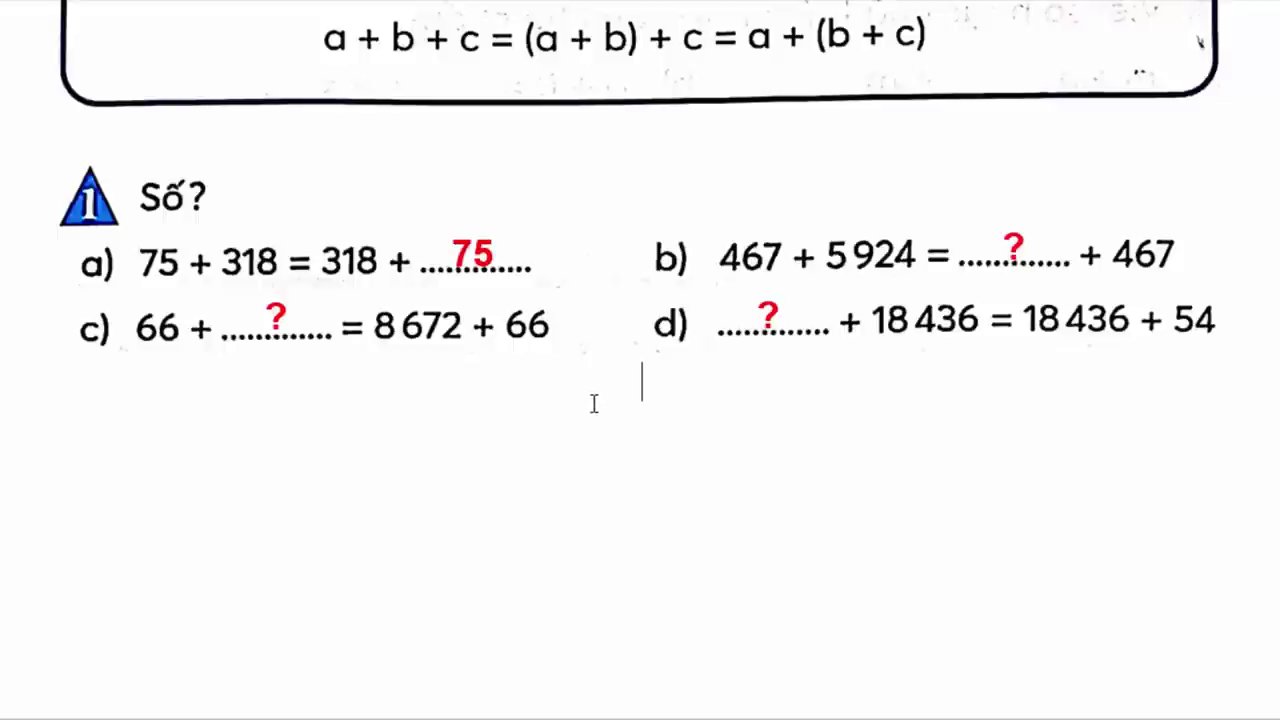
Dạng 2: Điền Dấu >, <, =
Dạng bài này kiểm tra xem các em có thực sự hiểu bản chất của tính chất giao hoán và kết hợp hay không.
Ví dụ: So sánh (2000 + 200) + 1975 và 2000 + (200 + 1975).
– Phân tích: Theo tính chất kết hợp, hai tổng này phải bằng nhau vì chúng chỉ khác nhau ở cách nhóm các số hạng: (2000 + 200) + 1975 = 2000 + (200 + 1975).
– Thực hiện: Dù có tính riêng từng vế, kết quả đều là 4175.
– Kết luận: Điền dấu “=”.
Dạng 3: Bài Toán Có Lời Văn Ứng Dụng
Toán học luôn gắn liền với cuộc sống. Hãy cùng xem xét một bài toán thực tế sau:
Mẹ mua 3kg gạo nếp, 30kg gạo tẻ và 2.7kg đậu xanh. Hỏi mẹ đã mua tất cả bao nhiêu kg?
- Phân tích: Đây chính là phép cộng tổng số kg: 3 + 30 + 2.7.
- Thực hiện: Có thể nhóm để tính: (3 + 2.7) + 30 = 5.7 + 30 = 35.7 kg.
- Kết luận: Mẹ đã mua tất cả 35.7 kg.
Luyện Tập Tổng Hợp Và Bài Tập Nâng Cao
Để củng cố kiến thức, chúng ta cùng làm một bài tập tổng hợp đòi hỏi sự cẩn thận.
Bài tập: Tính tổng số tiền từ các tờ tiền có mệnh giá: 52,000đ, 16,000đ, 28,000đ, 4,000đ.
– Phân tích: Chúng ta cần tính 52,000 + 16,000 + 28,000 + 4,000.
– Áp dụng tính chất: Có thể nhóm các số để tính cho thuận tiện:
1. Nhóm 1: (52,000 + 28,000) = 80,000
2. Nhóm 2: (16,000 + 4,000) = 20,000
3. Tổng: 80,000 + 20,000 = 100,000
– Kết luận: Tổng số tiền là 100,000 đồng.
Cách nhóm này giúp chúng ta tính nhẩm nhanh chóng và tránh được những nhầm lẫn khi cộng nhiều số có nhiều chữ số. Đây là bước đệm quan trọng để các em tự tin giải quyết các bài toán phức tạp hơn, như các bài toán về phép trừ có nhớ trong phạm vi lớn.
Kết Luận
Qua bài học hôm nay, chúng ta đã cùng nhau khám phá hai tính chất “chìa khóa” của phép cộng: tính chất giao hoán (a + b = b + a) và tính chất kết hợp ((a + b) + c = a + (b + c)). Những tính chất này không phải là lý thuyết khô khan, mà là công cụ đắc lực giúp các em:
– Tính toán nhanh hơn bằng cách tìm và nhóm các số hạng phù hợp.
– Giải toán linh hoạt hơn, đặc biệt với các bài toán dài hoặc có nhiều số hạng.
– Hiểu sâu bản chất của phép toán, từ đó xây dựng nền tảng vững chắc cho những kiến thức toán học cao hơn.
Hãy thường xuyên luyện tập với nhiều dạng bài tập khác nhau để thành thạo các tính chất này. Khi đã nắm vững, các em sẽ thấy toán học thật sự thú vị và hữu ích trong đời sống hàng ngày. Chúc các em học tập thật vui và hiệu quả!
