Chào mừng các em học sinh lớp 8 đã quay trở lại với kênh giải toán “Kết nối tri thức với cuộc sống”! Hôm nay, chúng ta sẽ cùng nhau đi sâu vào một dạng bài tập quan trọng và thường gặp trong chương trình Đại số: Quy đồng mẫu thức các phân thức. Bài viết này sẽ hướng dẫn chi tiết cách giải Bài 615, trang 14, sách Toán 8 Tập 2, giúp các em không chỉ nắm được cách làm mà còn hiểu sâu bản chất để tự tin áp dụng kiến thức.

Bài toán quy đồng mẫu thức là nền tảng cho nhiều phép tính phức tạp hơn như cộng, trừ phân thức đại số. Nếu nắm vững phần này, các em sẽ thấy những bài toán phía sau trở nên dễ dàng và hệ thống hơn rất nhiều. Hãy cùng bắt đầu với từ khóa tìm kiếm bài học hôm nay: “Bài 615 trang 14 Toán 8 tập 2 Kết nối tri thức”.
Phần 1: Giới Thiệu Chung Về Dạng Bài Và Phương Pháp
Trước khi đi vào bài tập cụ thể, chúng ta cần nhớ lại mục đích của việc quy đồng mẫu thức: Biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức, từ đó thuận tiện cho việc so sánh hoặc thực hiện các phép tính.
Quy trình chung gồm 3 bước then chốt:
1. Phân tích các mẫu thức thành nhân tử (nếu có thể).
2. Tìm mẫu thức chung (MTC). Đây là bước quan trọng nhất, MTC phải chia hết cho tất cả các mẫu thức đã cho.
3. Tìm nhân tử phụ của mỗi mẫu thức và nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Việc học toán, đặc biệt là đại số, đòi hỏi sự kiên nhẫn và luyện tập thường xuyên. Đừng ngại nếu lần đầu tiếp cận thấy phức tạp, hãy dành thời gian phân tích kỹ từng bước như hướng dẫn dưới đây. Bạn có thể tham khảo thêm các bài viết về tính chất cơ bản của phân số để có nền tảng vững chắc hơn.
Phần 2: Hướng Dẫn Giải Bài Tập 615 – Câu A
Đề bài cho hai phân thức:
1. ( \frac{1}{4xy^2} )
2. ( \frac{5}{6x^2y} )
Yêu cầu: Quy đồng mẫu thức hai phân thức trên.
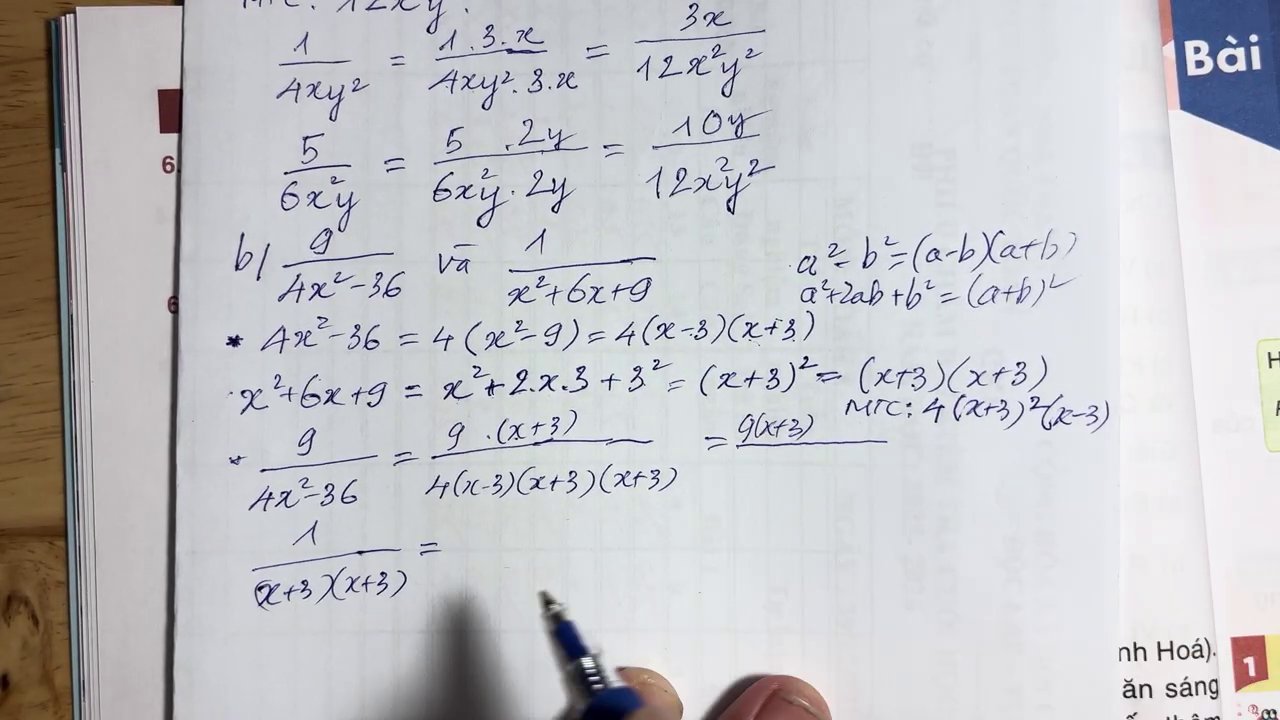
Bước 1: Tìm Mẫu Thức Chung (MTC)
– Phân tích các mẫu thức:
– Mẫu thức thứ nhất: ( 4xy^2 = 2^2 \cdot x \cdot y^2 )
– Mẫu thức thứ hai: ( 6x^2y = 2 \cdot 3 \cdot x^2 \cdot y )
– MTC cần chứa:
– Hệ số: Là BCNN của 4 và 6, tức là 12.
– Nhân tử x: Lấy lũy thừa với số mũ cao nhất là ( x^2 ).
– Nhân tử y: Lấy lũy thừa với số mũ cao nhất là ( y^2 ).
Vậy, MTC = ( 12x^2y^2 ).
Bước 2: Tìm Nhân Tử Phụ Và Quy Đồng
– Phân thức thứ nhất (( \frac{1}{4xy^2} )):
– Mẫu thức đang có: ( 4xy^2 )
– Để thành MTC ( 12x^2y^2 ), ta cần nhân thêm: ( 3x ) (vì ( 4xy^2 \cdot 3x = 12x^2y^2 )).
– Nhân tử phụ là 3x. Nhân cả tử và mẫu với 3x:
( \frac{1}{4xy^2} = \frac{1 \cdot 3x}{4xy^2 \cdot 3x} = \frac{3x}{12x^2y^2} )
- Phân thức thứ hai (( \frac{5}{6x^2y} )):
- Mẫu thức đang có: ( 6x^2y )
- Để thành MTC ( 12x^2y^2 ), ta cần nhân thêm: ( 2y ) (vì ( 6x^2y \cdot 2y = 12x^2y^2 )).
- Nhân tử phụ là 2y. Nhân cả tử và mẫu với 2y:
( \frac{5}{6x^2y} = \frac{5 \cdot 2y}{6x^2y \cdot 2y} = \frac{10y}{12x^2y^2} )
Kết luận câu A: Sau khi quy đồng, ta được hai phân thức: ( \frac{3x}{12x^2y^2} ) và ( \frac{10y}{12x^2y^2} ).
Phần 3: Hướng Dẫn Giải Bài Tập 615 – Câu B
Câu B phức tạp hơn với hai phân thức có mẫu thức cần phân tích:
1. ( \frac{1}{4x^2 – 36} )
2. ( \frac{1}{x^2 + 6x + 9} )
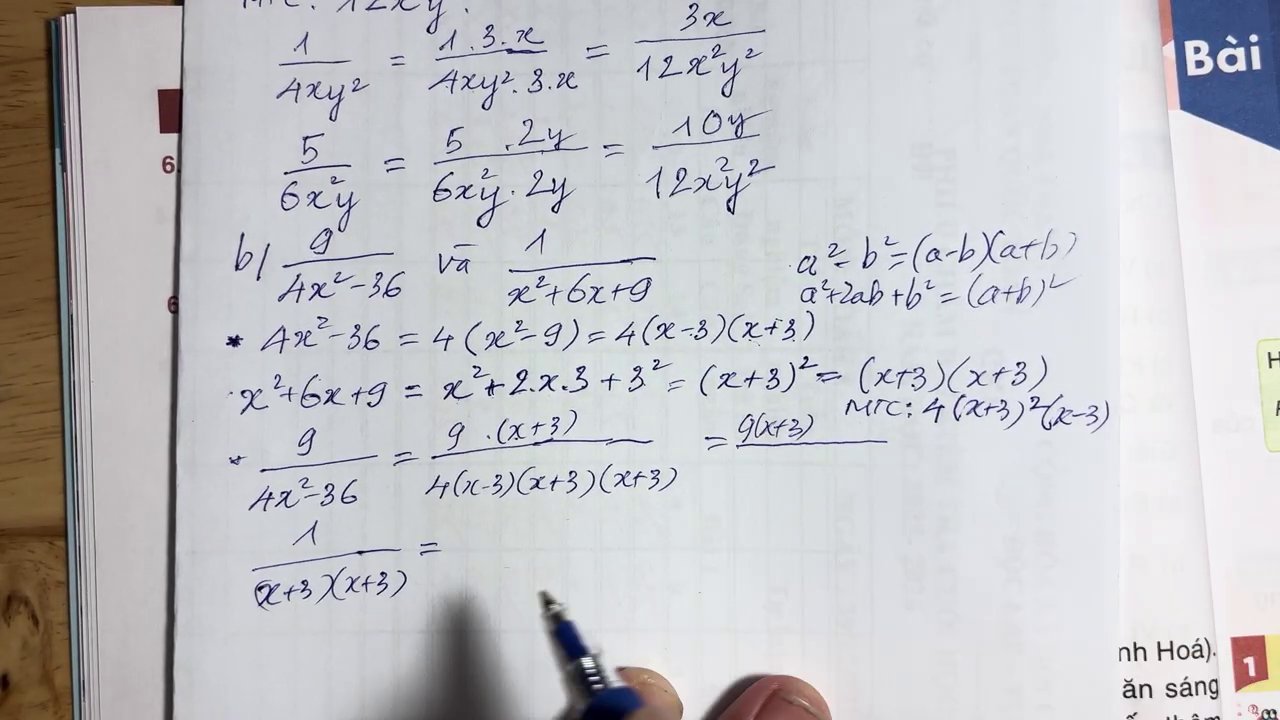
Bước 1: Phân Tích Các Mẫu Thức Thành Nhân Tử
– Mẫu thức thứ nhất: ( 4x^2 – 36 )
– Đặt nhân tử chung: ( = 4(x^2 – 9) )
– Áp dụng hằng đẳng thức hiệu hai bình phương: ( x^2 – 9 = (x – 3)(x + 3) )
– Vậy: ( 4x^2 – 36 = 4(x – 3)(x + 3) )
- Mẫu thức thứ hai: ( x^2 + 6x + 9 )
- Nhận dạng hằng đẳng thức bình phương của một tổng: ( = (x + 3)^2 )
Bước 2: Tìm Mẫu Thức Chung (MTC)
Từ các nhân tử đã phân tích:
– Mẫu 1: ( 4 \cdot (x – 3) \cdot (x + 3) )
– Mẫu 2: ( (x + 3)^2 )
MTC cần chứa:
– Hệ số: 4.
– Nhân tử (x – 3): có mặt trong mẫu 1.
– Nhân tử (x + 3): lấy lũy thừa với số mũ cao nhất là ( (x+3)^2 ).
Vậy, MTC = ( 4(x – 3)(x + 3)^2 ).
Bước 3: Tìm Nhân Tử Phụ Và Quy Đồng
– Phân thức thứ nhất (( \frac{1}{4(x-3)(x+3)} )):
– So với MTC, mẫu thức này thiếu một nhân tử ( (x+3) ).
– Nhân tử phụ là ( (x+3) ). Nhân cả tử và mẫu:
( \frac{1}{4(x-3)(x+3)} = \frac{1 \cdot (x+3)}{4(x-3)(x+3) \cdot (x+3)} = \frac{x+3}{4(x-3)(x+3)^2} )
- Phân thức thứ hai (( \frac{1}{(x+3)^2} )):
- So với MTC, mẫu thức này thiếu nhân tử ( 4(x-3) ).
- Nhân tử phụ là ( 4(x-3) ). Nhân cả tử và mẫu:
( \frac{1}{(x+3)^2} = \frac{1 \cdot 4(x-3)}{(x+3)^2 \cdot 4(x-3)} = \frac{4(x-3)}{4(x-3)(x+3)^2} )
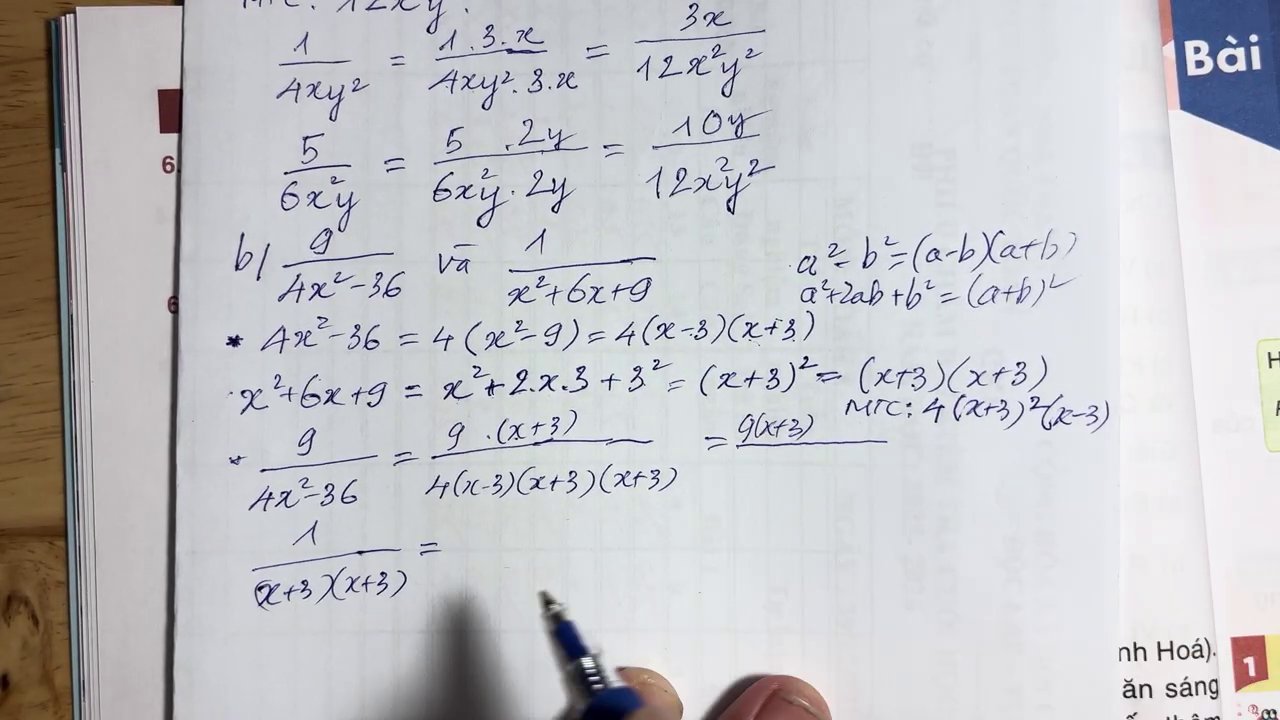
Kết luận câu B: Sau khi quy đồng, ta được: ( \frac{x+3}{4(x-3)(x+3)^2} ) và ( \frac{4(x-3)}{4(x-3)(x+3)^2} ).
Phần 4: Những Lưu Ý Quan Trọng Và Kinh Nghiệm Học Tập
Qua hai ví dụ trên, có thể thấy bước phân tích mẫu thức thành nhân tử là then chốt. Nếu phân tích sai, toàn bộ các bước sau sẽ sai theo. Hãy luyện tập thành thạo 7 hằng đẳng thức đáng nhớ và các phương pháp phân tích đa thức.
- Luôn kiểm tra kỹ MTC: MTC phải chia hết cho từng mẫu thức ban đầu. Một mẹo nhỏ là sau khi tìm được MTC, hãy thử chia MTC cho từng mẫu thức xem có phép chia hết không.
- Đừng quên nhân cả tử và mẫu: Tính chất cơ bản của phân thức là khi nhân (hoặc chia) cả tử và mẫu với cùng một đa thức khác 0, ta được một phân thức bằng phân thức đã cho. Quy đồng mẫu thức chính là ứng dụng của tính chất này.
- Học từ dễ đến khó: Hãy bắt đầu với những bài có mẫu thức đơn giản, sau đó mới nâng dần độ phức tạp. Việc luyện tập nhiều sẽ giúp bạn nhận diện dạng bài và thao tác nhanh hơn. Bạn có thể xem thêm các bí quyết giải toán tư duy từ cơ bản đến nâng cao để rèn luyện tư duy hệ thống.
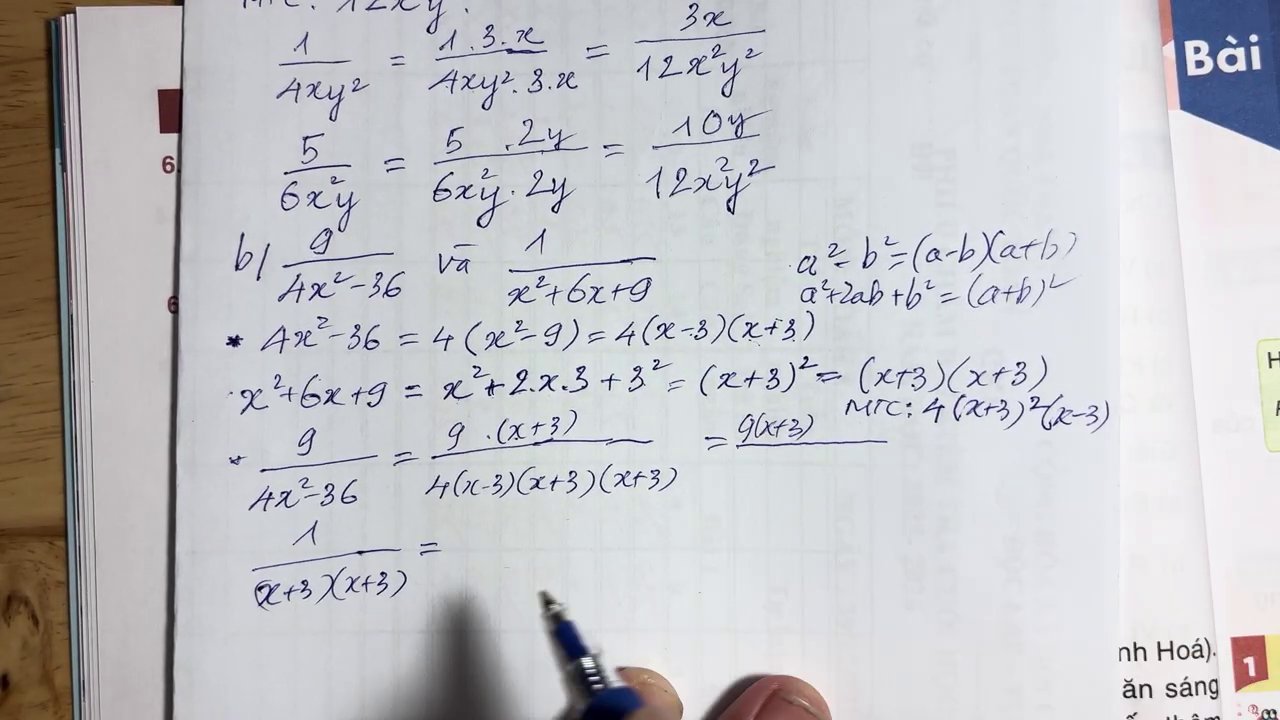
Kết Luận
Bài 615 là một bài tập điển hình, đầy đủ các bước để rèn luyện kỹ năng quy đồng mẫu thức phân thức. Hy vọng với hướng dẫn chi tiết trên, các em học sinh lớp 8 đã có thể tự mình giải quyết dạng toán này. Hãy nhớ:
1. Bình tĩnh phân tích mẫu.
2. Cẩn thận tìm MTC và nhân tử phụ.
3. Kiên trì luyện tập thêm nhiều bài tập tương tự.
Toán học là một môn học của sự chính xác và logic. Mỗi lần vượt qua một bài toán khó, các em không chỉ có thêm kiến thức mà còn rèn luyện được tư duy giải quyết vấn đề – một kỹ năng vô cùng quý giá trong cuộc sống. Chúc các em học tập thật tốt và đừng quên đón xem những bài hướng dẫn tiếp theo trên kênh “Kết nối tri thức với cuộc sống” nhé!
